Examples of application to bots

Managing Timestep spikes

As regards bots, I use the widespread solution of bounding the Timestep, with the following implementation:
Each bot has its own time BotTime, which is initialized to the GameTime at the start of a round.
Then, at the start of each bot update:
BotTimeStep= min( GameTime_n-BotTime_n-1, TIMESTEPMAX)
BotTime_n= BotTime_n-1 + BotTimeStep
BotTimeStep is the timestep value used in all bot thinking/acting code. TIMESTEPMAX= 100 milliseconds.

Introducing imperfection: alter the variable or add perturbations?

These solutions are very different.
Assumptions: during the bot frame computation of a view angle:
.The bot can retrieve the EngAngle_n-1 ouput by the engine the previous frame.
.The bot code delivers the perfect (ideal) value to the engine IdealAngle_n= f( position_n, ...)
.The bot code feds in the engine function: engine( IdealAngle_n), which results in EngAngle that will be available next frame.

Implementing a dynsyst altering variables ( an "in-the-loop" dydnsyst) would then look like:

Impl1:
IdealAngle_n= ...;
FinalAngle_n= dynsyst( IdealAngle_n, FinalAngle_n-1);
engine( FinalAngle_n);
In this implementation, the dynsyst is a blackbox inserted between the bot AI output and the engine input. If need be, you can in particular run the dynsyst code N times for a given IdealAngle, with the dydnsyst own Timestep being the engine Timestep/N, and the output forwarded to the engine being the dydnsyst output of the last( Nth)dynsyst commputation step.

Or
Impl2:
IdealAngle_n= ...;
FinalAngle_n= dynsyst( IdealAngle_n, EngAngle_n-1);
engine( FinalAngle_n);
In this second implementation, the engine is in the dynsyst loop, which requires a good knowledge on how the engine works, especially for stability analysis...so I do not use it.

Implementing a perturbation would look like:
IdealAngle_n= ...;
Perturbation_n=PertGenerator();
FinalAngle_n= IdealAngle_n+ Perturbation_n;
engine( FinalAngle_n);

1.One key point is that the dynsyst is most of the time placed within a closed loop, ie is dependent of the whole game loop. More precisely, this is obviously always the case for an implementation of type "Impl2". This also happens for "Impl1" whenever the IdealAngle computation in the bot AI depends on Engine outputs( usually the relative positions of the viewer and the target). This makes it trickier to handle than the perturbation model. This is why I would recommend using a perturbation model instead of an "in-the-loop" dynsyst if possible.
Unfortunately, only an "in-the-loop" dynsyst will be able to simulate the player in term of reaction time ( for detecting and execution), mouse speed and acceleration bounds, etc...

2.the "in-the-loop" dynsyst may unduly alter the behaviour of the game.
For example, with the "Impl2", if the engine adds a perturbation( like recoil) to the bot input, the dynsyst will detect an error and compensate for it, whereas a real player would most probably not be able to do that.
Note: in the recoil example, the only solution I see is to use (EngAngle-EngRecoil) as feedback instead of EngAngle, so that the dynsyst "does not see" the recoil.

3.As regards "in-the-loop" dynsysts, where they are placed in the code may give seemingly equivalent but actually different results.
For example, assuming the dynsyst is a simple first order filter and one wants to bound the speed.
One can implement a rate bounder within the dynsyst itself; the FinalAngle speed will then be bounded in all case.
Or one can "preliminary" bound the speed of IdealAngle as:
IdealAngle_n= ...;
BoundedRateIdealAngle_n= rateBounder( IdealAngle_n, BoundedRateIdealAngle_n-1..);
FinalAngle_n= dynsyst( BoundedRateIdealAngle_n, FinalAngle_n-1);
In that case, FinalAngle will only "see" IdealAngle commands as ramp inputs, which will also bound the speed as required, but the response curve will be different on a step change on IdealAngle from the first choice.
Moreover, for Impl2, FinalAngle speed is not bounded when the dynsyst reacts to a perturbation on EngAngle.

4.Dynsysts, and especially 2nd order dynsysts are fairly flexible.
For example, by assigning different parameters, one may simulate the cool-handed player ( damping> 0.7) or the panicked player trying to shoot its enemy stabbing him while "dancing" around him ( damping< 0.3). But the dynsysts alone feel too deterministic. Especially in the last situation, introducing noise seems to me to be a better choice.
Randomly varying the dynsyst parameters would bring a bit of a change, but I would think that fast and big variations, except for a situation change as in the example, would result in an irrealistic behaviour( but I did not try).

Perturbations

Using the 2^nd order noise generator with damping>=0.7 is my best choice when I want to introduce slowly varying errors.
ColoredNoise1 is still to jerky for me even with high smoothing, but is OK if its output is only used once in a while.
If the perturbation is event-triggered, changing the SigmaOut value over time starting when the event is triggered will provide a varying amplitude for the error.

Simulating a human player controlling the view angle through the mouse

Several points must taken into consideration.

Refining the objective

The basic goal is to have a bot which, viewed from outside by other human players , behaves like a human player.
This includes in particular its ability to place fast and accurate shots ( headshots in Counter-Strike), and this is the main focus here.
A more stringent goal is that, when a spectator looks through its eyes, the behavior is still human-like.
My focus is on the basic goal as it already raises enough problems, and is probably a necessary step to reach the second one.

Actually, what we want to simulate, letting aside decision making and control, should be adressed with two different systems:
1. One system which deals with the player viewed as a sensor.
This relates to a first phase of detection and identification ( probability of detection, detection reaction time), which is not addressed here.
Then it relates to the subsequent phase of evaluating the variables of interest ( inaccuracy of data).
"Estimators" dynsysts are used in that phase.
2. Another system, using data provided by the first for feedback along with AI ouputs for commands, which deals with the player viewed as an actuator.
This relates to the dynamic of mouse move ( muscles are involved,...), which includes reaction time, inaccuracy, speed, acceleration bounds,...
Still, for sake of simplicity, my design goal was to find a dynsyst that can simulate both.

A basic approach

Focusing on shooting, I assume one has got an idea of ts, the delay between detection and the first shot/hit.
One can then separate the issue of realistic shooting and view angle changes.
A trigger starts a timer that prevents the bot from shooting until "ts" seconds has passed.
View angles changes can then be as simple as being instantaneous, because it is the herabove timer that sets the key variable.
If a dynsyst is implemented, it must just insure that the view angle is equal or very close to the ideal one no later than "ts".
The initial error can never be greater than 180 degrees, so a speed bounder on ideal view angle with SPEEDBOUND>= 180/ts is a solution.
The problem is that using a timer becomes irrealistic when the target moves, for example if it starts strafing.
In my view, using a delay is appropriate for detection, but not for aiming moves and shooting, so this does not work.
The process is therefore to select a dynsyst that deals with the view angle, and decide on shooting ( assuming other AI constraints are OK) based on the resulting line of fire/sight passing close enough to the targetted spot.

The simple case: the bot and its target do not move

The simplest dynsysts are the rate ( or speed) bounder and the first order linear filter N1LL.
Focusing on headshot, and assuming the head is a sphere with radius 4, the time "tf" to move from the current view angle A0 to the ideal range around Ac> A0 is approximately, D being the distance to the target
.tf= (Ac-A0-4/D)/SPEEDBOUND for the speed bounder,
.tf= -Log(4/(D*(Ac-A0)))/k for the first order, which varies fast for low Ac-A0, but slowly for high Ac-A0.
I consider the first order to be closer to a player behaviour, with a settling time ST between 0.15 and 1.2 ( k=3/ST). If a speed bounder is deemed necessary, the SPEEDBOUND must then be high enough to not significantly override the linear first order effect.

I have used for some time filter N1LB on bot view_angles when the bot is looking at different non moving places in the world, ie when the target is not a precise point, but a general area around a point. I used different different parameters depending on its actual action : a "slow" filter when watching around while not moving and feeling safe, a "fast" one when expecting immediate threat to popup from one or more different places, or when moving and watching potential threat points coming into view along its move.
The bot moving generates an error but accuracy in those cases is not key( no shooting).

the bot and/or its view target move

Players seldom(!) move at constant speed along a circle centered on the viewer, ( which corresponds to what some properly designed dynsyst can handle, ie a constant rotation speed, ie a ramp, on input view angle ).
Players moving straight at constant speed is a more relevant assumption, but this means that the angle has nothing to do with the simple test inputs curves like step,ramp,...: it looks like an arctangent.
A way out of this problem is to design dynsysts based on straight move model with the help of Kalman filtering approach.
This is complicated, more "code intensive" and will not be addressed here.

My idea is then to select a dynsyst based on view angles, and test it once designed and tuned with an input view angle computed from a straight trajectory at constant speed, in order to get an idea of the error behavior and max value (see comparison below).

1. using a first order dynsyst
The problem is that an input IdleAngle varying at a constant speed generates an error in steady state.
For a very optimistic SettlingTime of 0.15 seconds, using N1LL_Ns filter with Timestep T= 0.03s , and a target player crossing the bot field of view at speed= 250 at distance D , the error is (250/D)*T*(1-A)/A with A= 1-exp(-3*0.03/0.15)=0.45 ie approx 9/D, whereas the headshot requires 4/D.
This solution does not work.
2. using a second order dynsyst
I did not encompass using a simple second order low-pass filter, as I can get, without increasing the order, a dynsyst designed to insure a null error on ramp input.
It is the N2KN_AS dynsyst which I currently use without bound on acceleration.
I use it now also for static targets.
Note: beware that dynsysts that generates overshoots will produce, if not taken care of in some way, an abnormal behavior whenever the input pitch is close to the [-90,90] bounds.

view angles variation consistency

A problem arises from the fact that azimuth and elevation ( yaw and pitch in Counter-Strike) should vary consistently.
If one uses a linear dynsyst for yaw and another one with the same parameters for pitch, both angles will close up to their respective input ( perfect) value at the same time. Behavior may even still be acceptable if the parameters are different, or the even if the dynsysts, while still linear, are different. But if using non linear dynsyst(s), behavior will on the contrary a priori be not acceptable.
For example, if the dynsysts are bounding the speed of the angles, one angle may reach its final value markedly earlier than the other.
I have tried 2 solutions.

Solution 1:Angle between vectors
I choosed the key variable to be the angle between the 2 vectors associated with the input (perfect) angles and the previous ouput angles. This angle would be input in any dynsyst that would reduce it to zero, and the new output angles derived from the resulting output. The view vector would then rotate around the cross-product of the input and previous ouput vectors. Two cases complicate the code: when the angle comes close to zero, and -nastier- when it is equal to 180 degrees ( which rotation vector should be used?).
Anyway this solution does not provide what we need. As an example, a bot looking slightly above the horizon to north and deciding to look slightly above the horizon to south would move its view vector in a vertical plane!

Solution 2: Combined variables
Keeping with the idea of dealing with only one variable and one dynsyst, I choosed a combined error from the yaw and pitch errors:
YawErr= yawInput_n- yawOutput_n-1;
PitchErr= pitchInput_n- pitchOutput_n-1;
CombError= sqrt(YawErr²+ PitchErr²);
I used a variation of a first order filter ( N1LB ) which reduces its input to zero ( high pass filter):
UpdatedCombError= dynsyst( CombError).
( Note:A first order works with an input (CombError) that cannot be negative because the updated output value is always between the input and the previous output.)
Getting updated yaw and pitch errors:
yawErr_n= YawErr* UpdatedCombError/ CombError;
pitchErr_n= PitchErr* UpdatedCombError/ CombError;
and finally get updated yaw_n and pitch_n as:
yawOutput_n =yawInput- yawErr_n
pitchOutput_n =pitchInput- pitchErr_n

Some ideas for extensions...
-Add a second subsequent filtering stage with separate linear filters on yawOutput_n and pitchOutput_n
-Add a second preceding filtering stage with separate linear filters before Combination
-Different weights for yaw and pitch -...
Afterthought: CombError looks like a distance which seems odd but angles variations are actually mouse moves in the xy plane. This lead me to a different frame of thinking, and consider simulating view_angles move by using solutions for path control in the xy plane.
Moreover, a human player does not drive the mouse in the x plane ( say pitch) with the same arm move than in the y plane ( say yaw). So yaw and pitch consistent moving may not be that hard a constraint after all.

This is why I currently use two separate N2KN_AS dynsysts for yaw and pitch ( with no acceleration bounds), with the speed estimation process bypassed when irrelevant (eg: switching targets ).

Comparison of solutions on a target moving straight at constant speed (with Counter-Strike parameters)

The dynsysts are applied to the bot yaw ( azimuth) angle; pitch angle( elevation) is constant=0.
The bot starts with yaw=0.
The target is moving horizontally at a speed=260 "units"/s ( a bot is approx 32 units wide), on a straight line which is D= 100 "units" away from the bot.
The target moves from left ( idealyaw= -90 degrees) to right ( idealyaw= +90).
The "metric error" is E= d*tan( output-input) where input= idealyaw), and d=dist(bot, target)= D/cos(idealyaw).
E less than 4 means a headshot is possible, E less than 16 means a body hit is possible.
N2KL and N2KN_AS work far better than the "classical" filters N1LL and N2LL. They allow for a body hit after 0.7 seconds, and sometimes for a headshot.
The "pure" non-linear filter N2NL, because the "parabolic speed bound" is not implemented, shows a null error -as expected- once the input stays within its speed and acceleration bounds.

Using perturbations

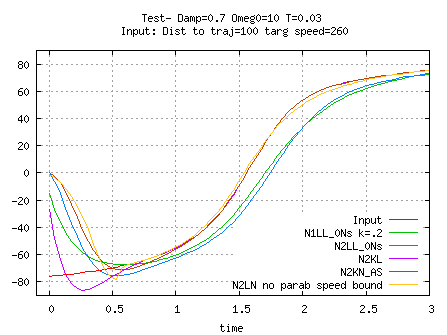
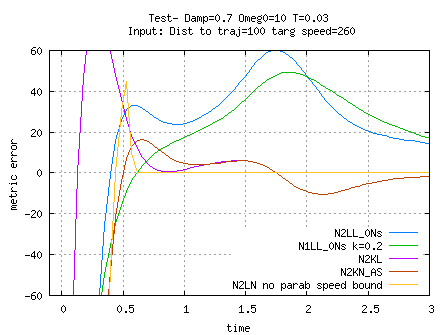
The N2KN_AS dynsyst seems to me to be the best solution, but I finally do not like the idea of destabilizing the dynsyst ( decrease damping down to .3 or .2) to model a nervous player.
Viewing the inability of a human player to point straight to its spot target as an inability to ever know the exact relationship between a mouse move on the desk and an angle on the screen, I wound up with the following model:
When aiming, the player systematically makes an error, implemented as a perturbation offset to the ideal view angle.
This perturbation is constant until the view angle comes close to the ideal one: at that time, the player evaluates the next mouse move to be performed and makes again an error.
The process is endlessly repeated, and converges as the perturbation is choosen to be a random coefficient with Mean=0 multiplied by abs( input-ouput).
One should note that adding a proportion of (input-ouput) actually alters the dynsyst stability, which is here a nice side effect.
Hence a nervous player will have a dynsyst with approximatively the same damping ( >=1.0 probably) and greater frequency ( faster), but will have a higher proportion for the perturbation.
The perturbation update is triggered by the condition ( working for constant speed targets):
abs((ideal_n-ideal_n-1)-(ouput_n-ouput_n-1))< Epsilon ( to be defined), and also when the target changes.
The underlying assumptions is that a human player is not 100% a continuous system, constantly evaluating, comparing all variables and thinking, reacting all the time on everything. I would rather compare the player to a multithreaded system, sharing limited resources ( like capacity of thinking/sensing focus)( anything on the Net on that topic?).
I did not go any further in designing this solution but preliminary testing indicates that it could be my ultimate best one.

Move/Speed control

In Counter-strike, actual speed is computed by the engine.
I do not like the implementation but I obviously cannot do much about it ( and there may be good reasons to do it that way that I do not know of- animation management maybe?).
Still, I tried and found another design, avoiding in particular the threshold on speed input value which creates problems to me in bots move control, and filterN2NLis what I came up with.
It only addresses speed value, not speed direction, though a complete solution would take the obvious correlation between speed and direction angles rate of change into account ( I did not like its implementation in CS either). This is a topic for "Bot Navigation".

Stopping distance
When moving straight and changing bot speed input setting to zero , speed dynamics in game-engines are such that the bot still moves on what I call the stopping distance before actual speed is zero.
This can reasonably, if not exactly, be modelled by first order , possibly non-linear, dynsysts like N1LL, N1LL_Ns, N1LA, N1LB. For the models told about hereabove, the speed decays as an exponential on some portion of its drop, or at constant rate ( constant deceleration). It is the case for Half-life ( see "Bot Navigation").
Knowing this stopping distance helps to better control bot move in several cases:
- when it must stops on a point, a line or a plane
- when it must avoid crossing a line or a plane; in that case, a stopping distance check can trigger a safe direction change ( ie early enough in all cases).
- when, in bot navigation, it must know when to switch from its current path segment to the next.
Here are several models for game-engine speed dynamics.
is the bot speed input to the engine.
The position follows a simple integration scheme as = + T* or = + T*
is the speed when is set to zero.
Linear model( N1LL): = + A* ( - ) then stopping distance is **/A.
Linear model( N1LL_Ns): = + A* ( - ) then stopping distance is **(1-A)/A.
Constant deceleration model with N= (int)( / Decel*): = - N** Decel and = + T* then stopping distance is N*( - 0.5* Decel*)- 0.5* Decel * (N)²
Constant deceleration model: = - T* Decel and = + T* then stopping distance is
N*( - 0.5* Decel*)- 0.5* Decel * (N)²+ .

Calculating speed and position for speed decay behaviour combining a mix of these models can be done; formulas for a first order linear filter giving the integral of the output on a step input are provided in N1LL and N1LL_Ns. Doing the same for constant deceleration and using the formulas piece-wise gives the answer, as can be applied to HalfLife:
. Half-Life model: for initial speed above \"stopspeed\" cvar, speed decays exponentially, then in all cases the speed drop is linear; code is provided in \"Bot Navigation\".
A more practical solution can be to use a approximate model ( the linear one is the simplest), providing it is conservative, ie approximate stopping distance > true stopping distance.