The "filter going weird" syndrom

Wrong tuning parameters

The widespread process to get a numerical system is the following: start from a continuous dynsyst equations, tune its parameters to meet damping and responsiveness requirements, then numerize it to get a numerical system. This process is wrong.
The following example is not a theoretical proof but calls upon common sense.
the 1^st order continuous filter equation is dx/dt= k*(u-x), where k ≥ 0, but with no upper bound.
Numerizing using a simple integration scheme results in the numerical filter:
X_n= X_n-1+ A* ( U_n-1- X_n-1) with A= k*T, T being the Timestep ie the delay between 2 updates.

Now let us re-write this as:
X_n= (1-A)* X_n-1+ A* U_n-1
X_n then shows as a weighted average of X_n-1 and U_n-1, which implies that A should be such as 0 ≤A ≤ 1.
Hence k=A/T has now an upper bound value equal to 1/T, and this constraint is overlooked in the numerizing process.
Actually, A= 1- K with K computed as in 1^st order stationary linear system is not even equal to k*T. The discrepancy is even worse for 2^nd order filters.

Timestep/Framerate issues

Effect of sampling

As the game Timestep T( ie the time between 2 updates or frame period, ie inverse of frame per second) is somewhere between 10 milliseconds and 100 milliseconds, and as a human player reaction time which we want to simulate is, in case of urgency, around several hundredth of seconds, one must take particular care of the behavior of a numerical dynsyst for dynsyst reaction time set close to Timestep value.
This enforces constraints on the numerical dynsyst dynamic characteristics relative to the timestep T and basically rules out the usual approximation exp(-k*T)= 1-k*T.
If not cared for, the dynsysts behavior will degenerate, which may or may not be acceptable depending on the designer's standpoint ( do your own testing!).

Note: First order systems ( including then the case of over-damped second order systems as they can be split into 2 first order systems) do not show this syndrom, unless the parameters do not meet the stability rule requirements. The focus will then be on second order damped-oscillations systems.

Assuming that the Timestep is constant , eventhough the 2^nd order numerical dynsyst parameters K0 and K1 are computed using the formulas for a numerical dynsyst as in , a stable system can show a weird behavior, due to sampling.
Those who know about information theory( Shannon, frequency wrapping) will not be surprised that , to be safe in all cases, the natural (undamped) frequency ( in rad/s, not in Herz) ω₀ must be less than π/T ( π= 3.14...). If not, the shape of the output of a damped-oscillation system for a given input will vary widely (and wildly!) with ω₀ increasing.
This is all the more disturbing as the variation of the shape with increasing ω₀ seems to be random : sometimes with overshoot/oscillations, sometimes with none.
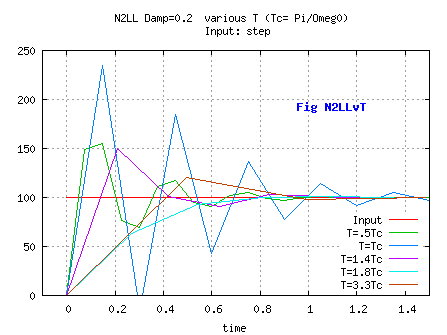
This happens if ω₀ is choosen regardless of the actual Timestep , and K0, K1 computed with an estimated/preset Timestep higher the actual one[ see Fig N2LLvT].

Let us assume that ω₀ is choosen so that ω₀ *(expected) Timestep< π, and K0, K1 calculated accordingly once and for all.
As the stability is set through K0 and K1, whenever the actual( constant) Timestep is different from the expected Timestep , the actual ω₀ will vary as the inverse of Timestep but output curves will look the same ( in particular, damping will stay the same). It will look like the time axis is dilated/contracted.

Timestep variations

All the theory that I know of deals with constant time steps T( except Kalman filtering, but it deals with observation problems, but not with control problems). In games, I would say that T suffers from two types of variations :
-small variations of T that ( could) occur almost every frame, and which are considered as acceptable as they do not spoil the gaming experience.
-huge variations of T from time to time ( "spikes").

small variations of T

I have the following options in mind:
1. to recompute K0 and K1 while checking that ω₀< π/Timestep ( using exact calculations, or interpolation in a preset table, or use Taylor expansion around an average Timestep, ...). This is anyway not perfect for filters of order > 1.
Re-computations can be performed every Timestep, or only when the Timestep is markedly different that the one used previously to compute the parameters. The Timestep value for parameter computation can be the current ( ie "instantaneous") value or a filtered Timestep ( using a 1^st order low-pass filter like N1LL_Nsfor example).
2. to leave K0, K1 and derived parameters unchanged but accept ω₀ variations, ie a responsiveness varying with Timestep. This is obviously by far the simplest solution but probably not acceptable for large Timestep variations.
3. to run the filter with its own constant sampling period TimeStepFilter < (global) Timestep, with adjustements when Timestep/ TimeStepFilter varies and/or is not an integer.

Most of the dynsysts proposed in PSEUDO-CODE/CODE have been tested with T uniformely random between 0.1 sec and 1.0 sec and changing every step ( which is quite severe I think) to see how robust they are:
-Dynsysts with order greater > 1 are more sensitive than first order dynsysts,
-Degeneracy increase with greater inputs variations with time,
-Endly, degeneracy is worse when bounding acceleration.

Huge variations of the Timestep T from time to time ( "spikes").

The solution depends on the wanted behavior in this case, and I do not have a generic one.
If the time step is large compared to the dynsyst reaction time, one may want
- to artificially bound the Timestep, which is a widespread solution in games,
- to consider that the dynsyst has reached its steady state.

Letting Output=Input comes to mind as the obvious practical implementation, but it is not that simple: for a first order linear low-pass filter with input being a ramp ( ie constant speed),the steady state results in Input-Output being a non null constant [ see N1LL]

- to consider that the dynsyst variables must be frozen to their last value,
- to consider that the dynsyst has to be re-initialized ( but how ?),
- to let the dynsyst run but alter temporarily its dynamics characteristics to keep on fullfilling the constraints related to the sampling rate,
- to let the dynsyst run "on its own" in cases where variable time steps of any value are dealt with by design ( Kalman filters, in particular dead reckonning).

Numerical instability

Wrongly designed non-linear dynsysts may show undesirable oscillations, especially when the output becomes close to the input. This should not happen with the dynsyst proposed in the PSEUDO-CODE/CODE section.