Definitions and assumptions

RefFrame

The reference frame RefFrame is 0xyz, orthogonal and direct, attached to ground, where z is vertical \"pointing to the sky\".

Vector notation

Taking velocity as an example for a vector, vVel is the vector, uvVel is the normalized vVel, the vector modulus is mVel. Hence vVel= uvVel * mVel.
The projection on the horizontal plane of vVel is vVelh, the modulus of which is mVelh.
The 2 direction-angles of a vector will be prefixed by "a" ( for azimuth/yaw) in the horizontal plane , and "e" ( for elevation/pitch) in the vertical plane.
Then, for velocity
uvVelx= cos(aVel)* cos(eVel)
uvVely= sin(aVel)* cos(eVel)
uvVelz= sin(eVel)

mVelh= mVel * cos(eVel)
vVelhx= mVelh* cos(aVel)
vVelhy= mVelh* sin(aVel)

Solid in 3D space

The orientation of a solid is defined by the usual 3 Euler angles; Yaw ( or Heading) is a rotation around the world z-axis and is equal to zero when pointing like the RefRame x-axis, Pitch is around the resulting new y-axis ( which remains in the horizontal plane) and Roll around the new x-axis.
Unless stated otherwise, all angles are assumed to be in degrees and wrapped in [0 included, 360 excluded[.

Velocity, acceleration

vVel is the mobile ( bot) velocity relative to the ground, ie measured in RefRame.
aVel is the TrackAngle, ie the direction of velocity in the xy plane.
The acceleration vector is vAcc= dvVel/dt= vAccL+ vAccT, where
the longitudinal acceleration vAccL is dmVel/dt * uvVel, tangential to the trajectory.
the transversal acceleration vAccT is mVel* duvVel/dt, perpendicular to uvVel.

Yaw and aVel can be different( eg: a mobile moving backwards, or slipping sideways on icy ground)

Circular trajectory in 2D

With C representing the center of the turn, a circular trajectory is expressed
-either as CM= Radius= constant,
-or vVel•vCM= 0 ( dotprod(vVel, vCM)= 0) ie aVel= aPolarAngCM + Sgn* 90 degrees, the radius being undetermined.

The following relationships hold, with omega defined as daVel/dt:
omega= daVel/dt= mVel/R, where R is the turn radius.
the side-acceleration mAccT, by definition perpendicular to vVel, is:
mAccT= mVel* omega, and vAccT is directed towards C.
Hence a bound set on one bot variable among yaw speed omega, mAccT and radius R can be translated in a bound on either of the 2 other variables and can be considered as equivalent.
Still, we can expect a game engine to implement bounds
-on yaw speed; if not, one needs anyway to be introduced for the bot because human players cannot move the mouse at infinite speed,
-on mAccT, wich relates more to the physics of the mobile simulated by the engine (eg: no skidding limit); it reflects in particular the fact that the max yaw speed can usually be increased ( ie the min turn radius decreased) to some point by reducing speed mVel.
Bounds expressed as a radii will rather be reflecting constraints on the wished trajectory resulting from the 3d world geometry and bounding boxes/cylinders of bot/other objects.

Controls

Whatever the engine or bot AI variable X, if the player/the bot can issue a command ( eg through the keyboard or the mouse for a player) setting the value of that variable, it will termed as a control and prefixed with "U_" like U_X. This assumes that the game engine or a BotAI sub-system input by U_X can run a process directly or indirectly modifying X and striving to make it equal to U_X.
Controls offerred by the game engine ( or equivalents) start with UE_.

The mobile

The position of the mobile is denoted M(Mx, My).
Its local x-axis, ie its Forward-axis, points "in front" of it.
Its "propulsion/breaking" device ( the legs of the bot in Half-life) explicitely or implicitely creates acceleration along its Frwd-axis, ie it can modulate velocity along that axis by setting a velocity modulus command UE_mVel.
The velocity direction is controlled through changes in Yaw by setting values for UE_yaw, ie a rotation around the mobile local z-axis; backwards moves commands will still have a positive UE_mVel but with UE_yaw= U_aVel+ 180. A consequence is that, even if the velocity is zero, aVel can be defined as equal to Yaw(+0|+180).
In Half-life, for a human player, UE_mVel is set by depressing a keyboard button, and UE_yaw is indirectly controlled through the view-angle control, ie the mouse. For a bot, the engine function ( pfnrunPlayerMove()) expects an ideal ( or wished) velocity UE_vVel, which can be easily computed from a (UE_mVel, U_aVel) pair.
Unless stated otherwise, the velocity component on the z-axis vVelz is assumed to be managed either by the game-engine, or by a separate BotFunction.
Therefore the (UE_mVel= UE_mVelh, UE_yaw) pair, the (UE_vVelx, UE_vVely) pair and UE_vVel=UE_vVelh are considered as equivalent representations of game engine velocity controls.

A mobile reference to a point

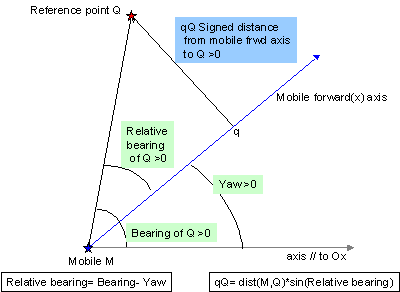
The position of a destination point is denoted Q.
The vector joining M to Q is vMS. the corresponding unitary vector is uvMQ.
The angle between the RefFrame and vMQh is the bearing denoted Bear.
The angle between the mobile Frwd-axis and vMQh is the relative bearing, denoted RBear.
Hence RBear= Bear- Yaw [see Figure].
The angle between the mobile velocity vVel and vMQh is denoted VelRBear.
Hence VelRBear= Bear- aVel.

A mobile reference to a directed line

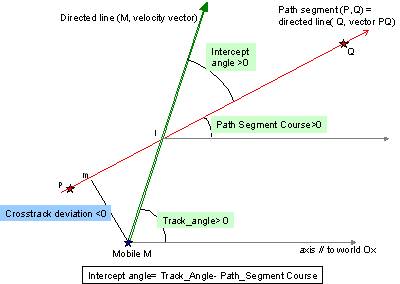
The directed line is defined by 2 points P and Q, or by Q and a unitary vector pointing towards Q.
The vector joining P to Q is vPQ. the corresponding unitary vector is uvPQ.
The angle between the RefFrame x-axis and vPQ is the directed segment Course denoted aPQ.
The angle between the mobile vVel and vPQ is the intercept angle, denoted XTDAngle.
Hence XTDAngle= aVel- aPQ= aVel- Course [see Figure].